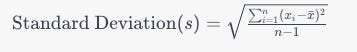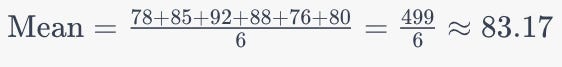What is the standard deviation and why is so important
Standard deviation is a statistical measure that quantifies the amount of variation or dispersion in a set of data points. It tells you how much individual data points deviate from the mean (average) of the data set.
In other words, it measures the spread or the "average distance" of each data point from the mean. A higher standard deviation indicates that the data points are more spread out from the mean, while a lower standard deviation indicates that the data points are closer to the mean.
The formula for calculating the standard deviation for a sample (n data points) is:
where:
xi represents each data point in the sample.
xˉ is the sample mean (average) of the data points.
n is the number of data points in the sample.
There is also the population standard deviation, which is used when the data set includes the entire population. The formula for the population standard deviation (with N data points) is similar but uses N instead of n−1 in the denominator.
Standard deviation is commonly used in various fields such as finance, engineering, social sciences, and more, to analyze and interpret data distributions and variability. It is an essential tool in statistical analysis and helps to understand the dispersion and uncertainty within a dataset.
Ok, an example, please!
Let's consider a simple example to understand standard deviation.
Let's say we have a dataset representing the scores of six students on a math test:
{78,85,92,88,76,80}
Step 1: Calculate the mean (average) of the dataset:
Step 2: Calculate the squared difference between each data point and the mean:
(78−83.17)^2 ≈ 26.69
(85−83.17)^2 ≈ 3.34
(92−83.17)^2 ≈ 78.25
(88−83.17)^2 ≈ 23.29
76−83.17)2^ ≈ 51.15
(80−83.17)2^ ≈ 10.07(
Step 3: Calculate the sum of the squared differences:
∑(xi−xˉ)^2 ≈ 192.79
Step 4: Divide the sum by (n - 1), where n is the number of data points (6 in this case):
Step 5: Take the square root of the variance to get the standard deviation:
So, the standard deviation for this dataset is approximately 6.21. This means that the scores of the students are, on average, about 6.21 points away from the mean score of 83.17.
The higher the standard deviation, the more dispersed the data points are from the mean, indicating more variability in the scores.
Conversely, a lower standard deviation suggests that the scores are closer to the mean, indicating less variability.
Where is used the standard deviation?
Standard deviation is used in various fields and applications to analyze data distributions and understand the variability or spread of data points. Some common areas where the standard deviation is used include:
Descriptive Statistics: Standard deviation is a fundamental measure in descriptive statistics. It provides insights into how spread out the data is from the average (mean). This helps to understand the typical distance of data points from the mean and how much the data deviates from the central tendency.
Finance and Economics: In finance, standard deviation is often used to measure the volatility or risk associated with an investment or portfolio. A higher standard deviation of returns indicates higher volatility and potential fluctuations in investment performance.
Quality Control: In manufacturing and process industries, standard deviation is used to monitor the variability of product quality or process performance. A high standard deviation in product measurements may indicate inconsistency or quality issues.
Social Sciences: Standard deviation is used in social sciences to analyze survey data, opinion polls, and other data sets to understand the spread of responses or attitudes within a population.
Natural Sciences: In fields such as physics, biology, and chemistry, standard deviation is used to assess the precision and accuracy of experimental measurements and to compare data sets.
Educational Assessments: In educational settings, standard deviation is used to evaluate the spread of student performance on exams and standardized tests, helping educators to assess the effectiveness of teaching methods.
Performance Evaluation: In business and sports, standard deviation can be used to measure the consistency and reliability of performance metrics, such as sales figures, player statistics, or team scores.
Quality Assurance: Standard deviation is used in quality assurance to monitor and control the consistency and variation in the production process.
Overall, standard deviation is a powerful statistical tool that provides valuable insights into the variability of data, helping researchers, analysts, and decision-makers make informed judgments and take appropriate actions based on the characteristics of the data distribution.
How can we apply standard deviation in Digital Marketing?
Imagine you are running an online advertising campaign to promote a product, and you have data on the number of clicks your ads received each day over a specific period. The goal is to measure the variability or fluctuation in the daily click-through rate (CTR) to understand how consistent the campaign's performance is.
Here's a simplified example with a 10-day period and the number of clicks received each day:
Day 1: 200 clicks
Day 2: 250 clicks
Day 3: 180 clicks
Day 4: 220 clicks
Day 5: 260 clicks
Day 6: 210 clicks
Day 7: 230 clicks
Day 8: 220 clicks
Day 9: 250 clicks
Day 10: 240 clicks
Step 1: Calculate the mean (average) of the daily clicks:
Mean = (200 + 250 + 180 + 220 + 260 + 210 + 230 + 220 + 250 + 240) / 10 = 230 clicks
Step 2: Calculate the squared difference between each day's clicks and the mean:
(200 - 230)^2 = 900
(250 - 230)^2 = 400
(180 - 230)^2 = 2500
(220 - 230)^2 = 100
(260 - 230)^2 = 900
(210 - 230)^2 = 400
(230 - 230)^2 = 0
(220 - 230)^2 = 100
(250 - 230)^2 = 400
(240 - 230)^2 = 100
Step 3: Calculate the sum of the squared differences:
Sum of Squared Differences = 900 + 400 + 2500 + 100 + 900 + 400 + 0 + 100 + 400 + 100 = 5800Step 4: Divide the sum by the total number of days minus 1 (9 degrees of freedom, as it is a sample):
Variance = 5800 / 9 ≈ 644.44Step 5: Take the square root of the variance to get the standard deviation:
Standard Deviation ≈ √644.44 ≈ 25.40In this example, the standard deviation of the daily clicks is approximately 25.40 .
This value indicates the level of variation or volatility in the click-through rate during the campaign.
A higher standard deviation suggests that the CTR varied significantly from day to day, while a lower standard deviation would indicate more consistency in the performance of the campaign.
Digital marketers can use standard deviation to assess the stability and predictability of their marketing campaigns. A more consistent campaign can help marketers make better decisions and optimize their strategies for better overall performance.